mapbox-gl画一条贝塞尔曲线

LiYajie: 2021-04-26 mapboxjsjs

效果如下

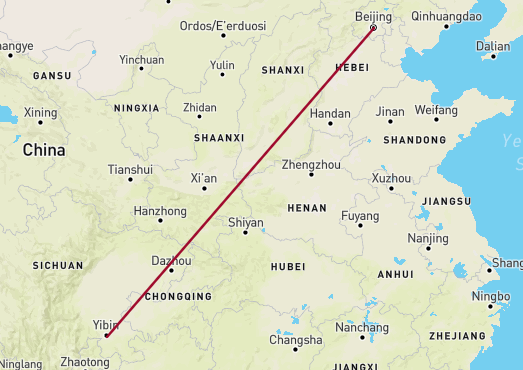
画直线

this.map = new Map(...)

this.map.addSource(id, {
  type: 'geojson',
  data: {
    type: 'FeatureCollection',
    features: [{
      type: 'Feature',
      properties: {},
      geometry: {
        type: 'Point',
        coordinates: [116.4111328125, 39.87601941962116] // 北京
      }
    }, {
      type: 'Feature',
      properties: {},
      geometry: {
        type: 'Point',
        coordinates: [104.67773437499999, 28.69058765425071] // 宜宾
      }
    }]
  }
})
this.map.addLayer({
  id: layerid,
  source: sourceid,
  type: 'line',
  layout: {},
  paint: {
    'line-color': '#f00',
    'line-width': 3
  }
})

画贝塞尔曲线

分析

1. 要想生成贝塞尔曲线, 最少需要三个点, 现在要根据这两个点来计算第三个点, 这样才能计算贝塞尔曲线
2. 想贝塞尔曲线比较对称, 第三个点需要在已知的两个点的中垂线上, 也就是说这三个点连接起来是一个等腰三角形
3. 通过下图来分析

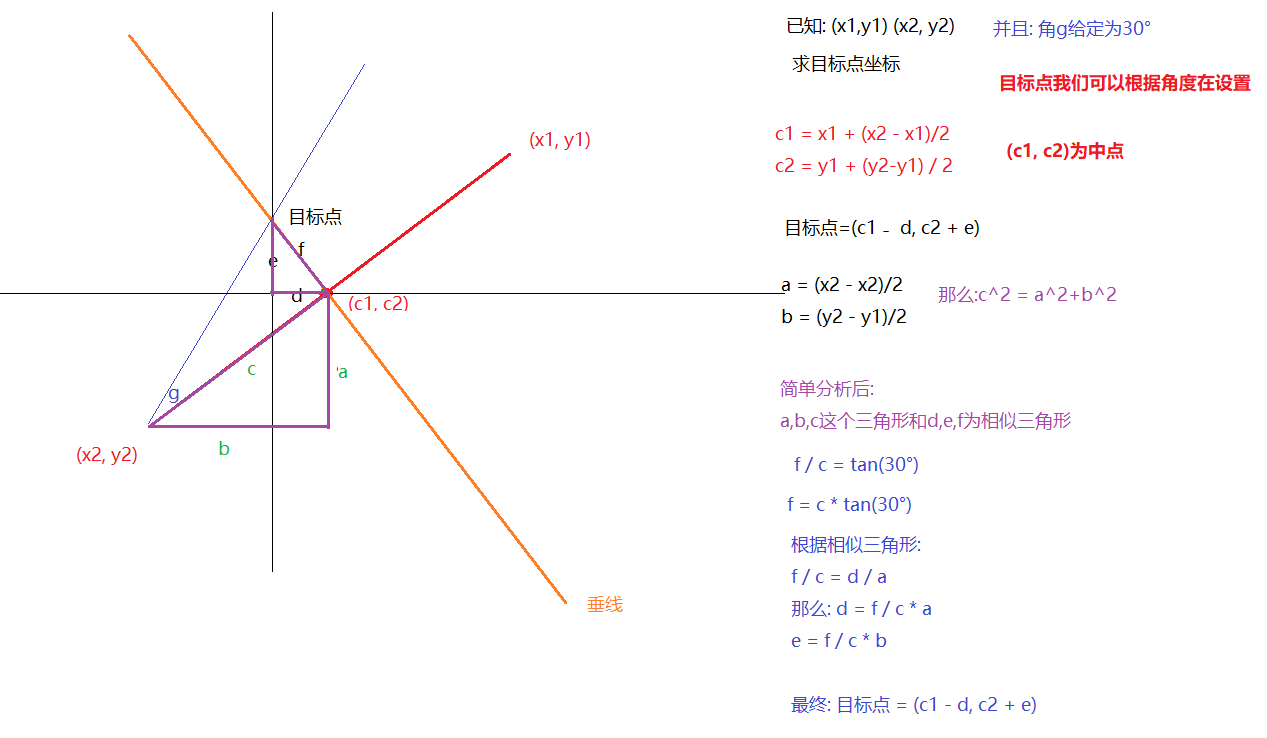
转换为js代码

// 根据两个点计算底角为30°的等腰三角形的顶点坐标
function calcCenterVertexPoint (start, end) {
  const deg = 30 // 角度为30度
  const x1 = start[0]
  const y1 = start[1]
  const x2 = end[0]
  const y2 = end[1]

  const xHalf = (x2 - x1) / 2
  const yHalf = (y2 - y1) / 2

  const centerX1 = x1 + xHalf
  const centerY1 = y1 + yHalf
  const center = [centerX1, centerY1]
  console.log(center)
  const xieLen = Math.sqrt(Math.pow(xHalf, 2) + Math.pow(yHalf, 2))
  const xieDui = xieLen * Math.tan(Math.PI * deg / 180)
  const xOffset = (xieDui / xieLen) * yHalf
  const yOffset = (xieDui / xieLen) * xHalf

  let r = [centerX1 + xOffset, centerY1 - yOffset]
  if (x1 <= x2) { // 这里这样处理是为了让曲线一直在上面
    r = [centerX1 - xOffset, centerY1 + yOffset]
  }
  return r
}

贝塞尔曲线就是根据图中的(x1, y1), 目标点, (x2, y2)这三个点生成的, 下图中: 北京(x1, y1), 宜宾(x2, y2), 三角形的顶点: 目标点

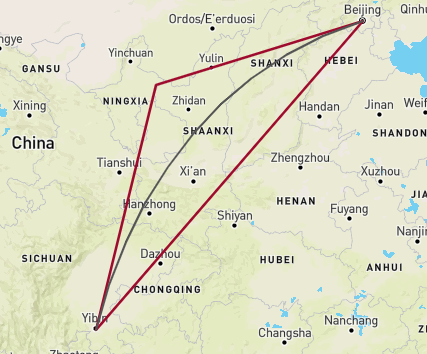
生成曲线的算法

const generatorCoors = function (poss, precision) {
  // 维度，坐标轴数（二维坐标，三维坐标...）
  let dimersion = 2

  // 贝塞尔曲线控制点数（阶数）
  let number = poss.length

  // 控制点数不小于 2 ，至少为二维坐标系
  if (number < 2 || dimersion < 2) {
    return null
  }

  let result = []

  // 计算杨辉三角
  let mi = []
  mi[0] = mi[1] = 1
  for (let i = 3; i <= number; i++) {
    let t = []
    for (let j = 0; j < i - 1; j++) {
      t[j] = mi[j]
    }

    mi[0] = mi[i - 1] = 1
    for (let j = 0; j < i - 2; j++) {
      mi[j + 1] = t[j] + t[j + 1]
    }
  }

  // 计算坐标点
  for (let i = 0; i < precision; i++) {
    let t = i / precision
    let p = {
      x: 0,
      y: 0
    }
    result.push(p)
    for (let j = 0; j < dimersion; j++) {
      let temp = 0
      for (let k = 0; k < number; k++) {
        temp += Math.pow(1 - t, number - k - 1) * (j === 0 ? poss[k].x : poss[k].y) * Math.pow(t, k) * mi[k]
      }
      j === 0 ? p.x = temp : p.y = temp
    }
  }
  result.push(poss[poss.length - 1])
  return result.map(a => [a.x, a.y])
}

const params = [{
  x: x1[0],
  y: y1[1]
}, {
  x: thridCoors[0], // 顶点
  y: thridCoors[1] // 顶点
}, {
  x: x2[0],
  y: y2[1]
}]
return generatorCoors(params, 10) // 生成10个曲线上的点